Sanotaan, että opettaminen opettaa parhaiten sitä, joka opettaa. Siksi ajattelinkin kokeilla erään matematiikan peruskurssi B:n demotehtävän selittämistä. Siinä kysymyksenä oli siis funktioiden sin(x) ja cos(x) väliin ilmestyvän "suikaleen" alan laskeminen määrätyn integraalin laskutoimituksella.
Integrointi on, niin kuin varmaan arvasittekin, erittäin outo asia minulle. Olin joskus kuullut integraali-sanan jossain, mutta en koskaan tiennyt mitä se tarkoittaa. Kun matikan B-peruskurssi alkoi, niin siinä siirryttiinkin jo heti integraalin määritelmiin niin että heikompaa saattoi hirvittää!
Mutta mennään laskuun. Käppyrä on siis tämän näköinen:
Sininen on cos(x) ja punainen sin(x). Tuosta pitäisi laskea ala, joka on merkitty vihreällä. Liikkeelle lähdetään niin, että ensin ratkaistaan pisteet, joissa funktiot leikkaavat toisensa. Tässä tarkasteltavaksi suikaleeksi voisi ottaa minkä tahansa suikaleen tuosta äärettömästä jatkumosta, mutta yksinkertaisuuden vuoksi kannattaa valita tuo y-akselia lähin.
Leikkauspiste määritellään siten, että molemmat funktiot ovat samanarvoiset jossain pisteessä, kirjoitetaan siis yhtälö
Tämän jälkeen jaetaan yhtälö cos(x):llä, jolloin saadaan
Sin(x) jaettuna cos(x):llä on yhtä kuin tan(x), joten kaava voidaan kirjoittaa muotoon:
Nyt tarvitsemme hieman trigonometriaa. Ajatellaanpa ja mietitään, että mikä pitää tangentin kulman arvo olla, että se saa arvon 1? Kun saamme tietää tuon maagisen kulman, saamme myös x:n arvon.
Kulmahan on 45°. x on siis ratkaistu, se on 45. Tämä on ensimmäinen leikkauspisteemme, mutta se pitää vielä muuntaa asteista radiaaneiksi. Muunto on helppo laskeakin, mutta kannattaa ajatella sitä niin, että 180° = π, joten 90° = π/2, joten 45° = π/4. Leikkauspiste 1 on siis π/4, ja ensimmäinen kuvakin sen todistaa.
Toinen leikkauspiste saadaan, kun katsotaan tangentin määritelmää. Kolmiosta
kulma α saadaan kaavasta
Se siis tarkoittaa sitä, että sekä x että y voivat olla joko positiivisia tai negatiivisia. Nyt otetaan avuksi neljään lohkoon leikattu yksikköympyrä:
Siitä pystyy suoraan näkemään, että kun x ja y ovat molemmat positiivisia ja kulma on 45° (= π/4), niin myös kun x ja y ovat molemmat negatiivisia, saa kulma arvon 45°. Tällöin yksikköympyrässä oleva kulma on 45° + 180° = 225°. Tämä on yhtä paljon kuin 5π/4. Siinä onkin toinen leikkauspisteemme.
Saimme nyt määrätyn integraalin rajat, joista alamme integroida. Kahden funktion välisen alan pisteestä a pisteeseen b saa näin kätevällä konstilla:
Tuossa f(x) on funktio, joka on "korkeammalla", ts. suurempi, tässä tapauksessa siis sin(x). Kun sijoitetaan saamamme luvut integraaliin
niin lasku onkin erittäin nopea, helppo ja mekaaninen toimenpide:
Vastaus on siis 2√2. Voilà!



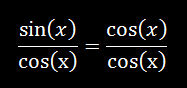








Ei kommentteja:
Lähetä kommentti