Nyt puhutaan matematiikasta. Lukion käyneille nämä asiat ovat selviä kuin pläkki, mutta itselläni ei ammattikoulussa nämä tulleet vastaan kertaakaan. Vasta yliopistossa olen oppinut, mitä kukin lukujoukko merkitsee. Opin tänään taas uuden lukujoukon lineaarialgebran demoissa, kun kysyin demojen vetäjältä, että kun reaaliluvut kuuluvat kompleksilukuihin niin onko kompleksilukujoukosta vielä suurempaa joukkoa. Se löytyy viimeisenä alla olevasta listasta.
Luonnolliset luvut

Symbolin alkuperä: N niin kuin Natural numbers
Mitä sisältää: kokonaisluvut nollasta ylöspäin, eli 0, 1, 2, 3,...∞
Kokonaisluvut

Symbolin alkuperä: saksan sanasta Zahlen, "numerot"
Mitä sisältää: kaikki kokonaisluvut, eli -∞..., -2, -1, 0, 1, 2, ...∞
Rationaaliluvut ℚ
Symbolin alkuperä: italian sanasta Quozient, "osamäärä"
Mitä sisältää: kaikki luvut, jotka voidaan esittää kahden numeron murtolukuna, esim. 1/2 tai 9/10
Irrationaaliluvut
Mitä sisältää: ne luvut, jotka eivät ole rationaalilukuja, esim. √2 tai π
Reaaliluvut
Symbolin alkuperä: sanasta Real
Mitä sisältää: kaikki desimaaliluvut, esim. -1, √2, 6006,45528
Mitä sisältää: kaikki luvut, jotka voidaan esittää kahden numeron murtolukuna, esim. 1/2 tai 9/10
Irrationaaliluvut
Mitä sisältää: ne luvut, jotka eivät ole rationaalilukuja, esim. √2 tai π
Reaaliluvut

Symbolin alkuperä: sanasta Real
Mitä sisältää: kaikki desimaaliluvut, esim. -1, √2, 6006,45528
Symbolin alkuperä: sanasta Complex numbers
Mitä sisältää: luvut, joissa esiintyy imaginääriyksikkö i eli √-1
Mitä sisältää: luvut, joissa esiintyy imaginääriyksikkö i eli √-1
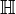
Symbolin alkuperä: keksijän nimestä Hamilton (Sir William Rowan Hamilton, 1805-1865)
Mitä sisältää: reaalilukujen ja kolmiulotteisen vektorin yhdistelmän, joka on muotoa t + xi + yj + zk, jossa t, x, y ja z ovat reaalilukuja ja i, j ja k kvaternioita
Mitä sisältää: reaalilukujen ja kolmiulotteisen vektorin yhdistelmän, joka on muotoa t + xi + yj + zk, jossa t, x, y ja z ovat reaalilukuja ja i, j ja k kvaternioita
Kvaternioita käytetään, tai on käytetty, demojen vetäjän mukaan translaatioihin eli jos halutaan siirtää jokin kappale matemaattisella käsittelyllä uuteen paikkaan avaruudessa. Jänniä juttuja! Tein vielä tällaisen kuvan asiasta.
Kuvasta voidaan sanoa, että luonnolliset luvut kuuluvat kokonaislukuihin, kokonaisluvut rationaalilukuihin jne. Ne ovat siis osajoukkoja isommalle ympyrälle. Matemaattisesti tämä merkitään osajoukko-merkillä ⊂:
 ⊂
⊂  ⊂ ℚ ⊂
⊂ ℚ ⊂  ⊂ ℂ ⊂
⊂ ℂ ⊂ 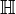
Myös irrationaaliluvut ⊂  ⊂ ℂ ⊂
⊂ ℂ ⊂ 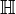
 ⊂ ℂ ⊂
⊂ ℂ ⊂ 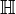
Tämänpäiväisissä demoissa merkkasin muuten ensimmäistä kertaa osoitustehtävän (eli pyydetään osoittamaan, todistamaan tai näyttämään jotain) tehdyksi. Nyt vasta, kakkosvuonna, olen päässyt kärryille siitä, miten jokin osoitetaan matemaattisesti. Kyseinen tehtävä oli tosin väärin, joten jääköön osoittamiset minulta vastaisuudessa tekemättä :D


Ei kommentteja:
Lähetä kommentti